Trucs et astuces sur LaTeX

Vous trouverez ici des trucs et astuces, explications et conseils de niveaux variés concernant LaTeX et son environnement. Certains sont originaux, d'autres biens connus des spécialistes mais pas encore assez diffusés.

Avertissement : cette page n'a pas été mise à jour depuis longtemps. Le conseils donnés ici ne sont peut-être plus tous d'actualité. Vous trouverez d'autres informations, plus à jour, sur la rubrique TeX de mon blog.

Navigation : cliquer sur un titre de section ramène au sommaire.

Sommaire

Quelques substitution de fontes utiles

La méta-famille de fontes latin modern remplace computer modern comme fontes standard. Sous LaTeX, on la charge en appelant le package lmodern. Elle souffre néanmoins pour l'instant deux défauts. Le premier est de n'être pas encore installée automatiquement dans la version de base de la plupart des distributions LaTeX. Elle est néanmoins facile à installer via le gestionnaire de paquets de votre distribution.

Le deuxième est de n'être pas encore aussi complète que computer modern : il manque par exemple les petites capitales grasses en famille romaine. L'objet de cette astuce est d'y remédier en allant chercher les fontes manquantes dans computer modern.

\rmfamily
\DeclareFontShape{T1}{lmr}{b}{sc}{<->ssub*cmr/bx/sc}{}
\DeclareFontShape{T1}{lmr}{bx}{sc}{<->ssub*cmr/bx/sc}{}

Le code précédent demande à LaTeX de substituer aux petites capitales (sc) grasses (b) ou grasses étendues (bx) de latin modern roman (lmr) les petites capitales grasses étendues de computer modern roman. Si vous utilisez la variante sub au lieu de ssub, LaTeX émettra un avertissement avant d'opérer la substitution. Enfin, le \rmfamily sert à s'assurer que les macros qui vont être modifiées par les deux lignes suivantes sont préalablement crées.

Remarque : cette méthode est contestable dans le sens où elle mélange allègrement deux familles de fontes. Cependant, vu la proximité entre cmr et lmr, ce mélange me paraît légitime ici, et constitue la moins mauvaise solution. Il convient de surveiller l'évolution de latin modern pour ne plus utiliser cette substitution dès qu'elle ne sera plus utile.

Connaître dynamiquement le mode de compilation

Comme vous le savez sans doute, la plupart des installations modernes utilisent le moteur pdfTeX pour toutes les compilations, y compris en mode dvi. Ce dernier fournit un moyen simple de déterminer au moment de la compilation si celle-ci a lieu en mode pdf ou dvi, afin par exemple de n'inclure que dans la version pdf certaines commandes spécifiques (voir « remplir les champs pdf » par exemple).

\ifnum\pdfoutput>0
(texte pour pdf)
\else
(texte pour dvi)
\fi

Vous pouvez bien sûr ommettre le \else et passer immédiatement au \fi. On rencontre parfois ce test sous la forme \ifnum\pdfoutput=1, ce qui marche souvent en pratique, mais le manuel de pdfTeX dit seulement que les valeurs négatives indiquent le mode dvi sans préciser de valeur précise pour le mode pdf.

Un peu hors sujet mais pas tout à fait, sachez que certains commandes détectent d'elle-mêmes le mode de compilation et en tirent les conclusion appropriées. C'est le cas par exemple de la commande \includegraphics{fichier} du package graphicx. Si vous prenez la précaution d'écrire le nom de fichier sans extension, et que deux versions (eps et pdf) sont trouvées, graphicx déterminera automatiquement quel type de fichier il convient d'insérer.

Remplir les champs pdf à la main

Les champs pdf (auteur, date, etc.) peuvent être remplis facilement avec les commandes fournies par le package hyperref (options de chargement du package ou commande \hypersetup). Il peut arriver que vous souhaitiez les remplir à la main, par exemple parce que vous ne souhaitez par charger hyperref pour si peu. Cela se fait facilement avec la primitive \pdfinfo de pdfTeX.

\ifnum\pdfoutput>0 \pdfinfo
{
/Title (Mon beau document) 
/Author (Moi) 
/Subject (Passionnant) 
/Keywords (mots, clefs)
}
\fi

L'exemple parle de lui-même. Remarquez que par prudence on n'insère ce code qu'en mode pdf (voir « pdf ou pas ? »), \pdfinfo causant un warning sinon. Remarquez aussi l'espace entre 0 et \pdfinfo : c'est une règle générale en TeX qu'il est prudent de laisser un espace entre un nombre et un nom de commande (autre que \relax) car sinon TeX va chercher à voir si la commande ne contient pas la suite du nombre, ce qui peut avoir des effets surprenants.

Les fantômes sont vos amis

La notion de fantômes en LaTeX est très simple : il s'agit de réserver de la place pour un objet, sans pour autant faire apparaître l'objet en question. Les fantômes sont souvent utilisés pour ajuster l'alignement. Ils y a trois types de fantômes obtenus respectivement par les commandes \phantom, \hphantom, et \vphantom.

L'exemple classique est celui de l'alignement des radicaux, illustré ci-dessous avec \[ \sqrt{x} + \sqrt{X} + \sqrt{\vphantom{X}x} \].

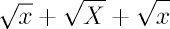
un exemple

La différence est fine et sera peut-être plus facile à observer sur un pdf (ou mieux, une version imprimée), mais on constate que la composition des deux radicaux de droite est plus homogène (ils sont alignés en haut) et donc visuellement plus satisfaisante.

Pour un autre cas d'utilisation des fantômes, voir le cas des délimiteurs non équilibrés.

Les fantômes sont un cas particulier d'une notion classique en typographie, celle de montants. En LaTeX, les montants sont obtenus en tant que réglures dont une dimension est nulle. Par exemple, \vphantom{X} a une action similaire à \rule{0pt}{\heightof{X}} (\heightof est fournie par le package calc). Il peut parfois être utile d'insérer directement une réglure de largeur nulle et de hauteur et profondeur déterminées à la main pour résoudre des problèmes délicats d'alignement.

Écraser verticalement des morceaux de formule

À l'inverse de l'astuce précédente qui vise à réserver de la place pour des éléments invisibles, on peut souhaiter que des éléments visibles n'occupent pas (ou moins) de place du point de vue de TeX, leur représentation graphique restant inchangée.

On réalise cela grâce à la commande smash, qui insère son argument comme un objet de hauteur et profondeur (voir le modèle de boîtes) nulles. Les variantes \smash[b] et \smash[t] (fournies par amsmath) n'annulent respectivement que la profondeur ou la hauteur.

Illustrons à nouveau ceci sur des racines avec le code suivant (utilisant amsmath) : \[ \sqrt{y} + \sqrt{x} + \sqrt{\smash[b]{y}} \]. Cette fois encore le phénomène est plus visible sur pdf ou résultat imprimé.

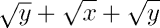
un exemple

Il convient d'utiliser ce genre de commande avec prudence car en mentant à TeX sur la taille des objets qu'il manipule, des risques de chevauchement visuels apparaissent.

Indices et exposants en folie

On a souvent envie de placer des indices ou exposants devant un symbole, par exemple pour la transposée d'une matrice. La solution de base consiste à placer ceux-ci sur un groupe vide, afin d'éviter qu'il n'aillent se coller au symbole précédent. Par ailleurs, on aura parfois intérêt à ajuster l'espace manuellement, par exemple en saisissant {}^t\!M.

Autour des opérateurs, on peut placer des indices et exposants avec la commande \sideset d'amsmath : \sideset{_a^b}{_c^d}\prod par exemple. Pour les autres symboles, on peut utiliser la commande \prescript de mathtools, qui fournit un alignement sur la droite, plus satisfaisant que celui de la solution du groupe vide : comparer {}^{12}_3 C et \prescript{12}{3}{C}.

Un peu en vrac dans cette section, je mentionne aussi la construction \substack qui permet de placer plusieurs lignes d'indices sous un opérateur, comme \sum_{\substack{(i, j) \in I^2 \\ i \neq j}}. Il y a aussi (à ne pas confondre) \stackrel pour placer des choses sur une flèche ou relation ( x \stackrel{f}{\mapsto} f(x)), et pour les cas plus compliqués \xrightarrow[bas]{haut} et ses variantes évidentes.

Enfin, on peut placer des « indices ou exposants centrés » avec \underset{bas}{symbole} et son frère \overset. Quelques exemples en vrac ci-dessous.

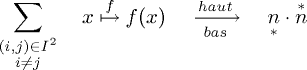
un exemple

Les huit styles mathématiques

TeX, et donc LateX, possède fondamentalement quatre styles mathématiques nommés \displaystyle, \textstyle, \scriptstyle et \scriptscriptstyle, chacun décliné en deux versions : normale et tassée. Il ne faut pas confondre les styles avec les modes (en-ligne ou hors-texte) même si ceux-ci sont reliés : le style par défaut du mode hors-texte est \displaystyle, celui du mode en-ligne étant \textstyle.

Ces styles déterminent de nombreux éléments de composition mathématiques, comme la taille des symboles, leur espacement, et la place des indices et exposants. On peut à tout moment changer de style par les commandes ci-dessus, qui agissent jusqu'à la fin du groupe ou jusqu'au prochain changement de style.

On contrôle indépendamment le placement des « limites  » avec \limits et \nolimits. Comparons ainsi $\sum_a^b$, \[\sum_a^b\], $\displaystyle \sum_a^b$, $\displaystyle \sum\nolimits_a^b$ et $\sum\limits_a^b$.

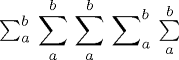
un exemple

Pour accéder manuellement à la variante tassée, on utilise la commande \cramped de mathtools, qui compose son argument en style tassé : cela change principalement la hauteur des indices et exposants. Il peut être utile de les compresser, par exemple pour préserver l'interlignage dans un paragraphe. L'effet est assez subtil, mais clair en comparant $2^{2^2}$ à $\cramped{2^{2^2}}$.

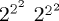
un exemple

Par ailleurs, lors de la définition d'une commande mathématique, vous pouvez prévoir des variantes selon de style mathématique courant avec la commande \mathchoice, qui prend 4 arguments, correspondants aux 4 styles mathématiques. Exemple :

\newcommand\undemi{\mathchoice
{\frac{1}{2}}
{1/2}{1/2}{1/2}
}

En style \displaystyle (par exemple une équation hors-texte) \undemi composera \frac{1}{2} et 1/2 dans tous les autres cas (par exemple une équation en-ligne ou un exposant en mode hors-texte).

Trois arguments contre eqnarray

  1. Typographiquement, eqnarray fait n'importe quoi. Plus précisément, il rajoute beaucoup d'espacement autour du symbole de relation, de façon injustifiée et incohérente avec les autres environnements mathématiques (ci-dessous equation, eqnarray puis align).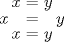
    un exemple
  2. Quand l'équation occupe toute la largeur de la page, eqnarray ne s'en rend pas compte et place le numéro d'équation en surimpression sur le texte. Les autres environnements standard, comme equation, ne présentent pas ce problème et placent le tag en-dessous. (À droite, align, à gauche, eqnarray avec \setlength\arraycolsep{2pt}.)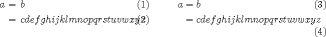
    un exemple
  3. Par ailleurs, eqnarray ne fonctionne pas correctement avec les commandes du package amsmath, incontournable pour composer les mathématiques. Par exemple, les commandes \tag et \intertext fonctionnent avec tous les environnements sauf eqnarray.

Pour ces raisons, eqnarray doit être considéré comme obsolète et je vous conseille de ne plus l'utiliser. Il est avantageusement remplacé par les environnements d'amsmath, notamment align.

Trois arguments contre l'usage de $$...$$

L'usage de $$...$$ pour passer en mode mathématique hors-texte n'a jamais été supporté par LaTeX : c'est un héritage de TeX. Les héritages de TeX ne sont pas tous mauvais, mais celui-ci est à éviter pour (au moins) les raisons suivantes.

  1. Il ne respecte pas les mécanismes de LaTeX, comme par exemple l'option fleqn de la classe standard article : cette dernière doit avoir pour effet d'aligner à gauche (au lieu de centrer) les équations hors-texte, mais les équations délimitées par $$ restent obstinément centrées.
  2. L'espacement vertical autour de l'équation est inconsistant. La plupart du temps, il sera correct, mais des comportements étranges peuvent survenir quand l'équation est précédée ou suivie de changements de paragraphes ou autres objets « complexes ».
  3. Enfin, tous les packages bien faits pour LaTeX supposent que vous utilisez les constructions standard de LaTeX, et risquent donc de ne pas fonctionner avec $$. C'est le cas d'amsmath, et par exemple, de sa commande \tag.

Les environnement standard prévus par LaTeX pour les mathématiques hors-texte sont displaymath, equation* et \[...\] : le dernier n'est guère plus long à taper que $$ et rend par ailleurs le source plus lisible.

Trouver la documentation

LaTeX, comme la plupart des systèmes ouverts et développés par ses utilisateurs, est accompagné d'une quantité impressionnante de documentation disponible en ligne. La quasi totalité des packages LaTeX est accompagnée d'une documentation spécifique, qu'il faut savoir trouver.

Selon la distribution LaTeX, une plus ou moins grande partie de cette documentation est installée avec les packages : TeXlive installe toujours la documentation, sous MikTeX il faut parfois le demander spécifiquement (via le gestionnaire de packages). Cette documentation est très facile à trouver grâce à l'outil texdoc. Par exemple, sous TeXlive/linux, taper texdoc xcolor dans un terminal ouvre immédiatement la documentation en pdf d'xcolor.

Cette documentation est aussi disponible en ligne sur le CTAN. Parmi les modes de recherche proposés, vous pouvez rechercher de la documentation par mots-clés ou nom de package. Vous pouvez aussi trouver des tutoriels ou documentations non spécifiques à un packages dans la section documentation du catalogue TeX en ligne.

Par ailleurs, les distributions sont aussi accompagnées de leur propre documentation, décrivant l'organisation des fichiers, les outils de bases, variables d'environnement, etc. Cette documentation se trouve sous plusieurs formes et/ou langues, par exemple aux endroits suivants (resp. TeXlive et MiKTeX).

Program Files/MiKTeX 2.5/doc/miktex/manual/index.html
Program Files/MiKTeX 2.5/doc/miktex/miktex.pdf
/usr/share/doc/texlive-doc/french/texlive-fr/live.html
/usr/share/doc/texlive-doc/english/texlive-en/live.pdf

Installer des packages à la main (cas facile)

La plupart du temps, utilisez les mécanismes de gestion de packages de votre distribution LaTeX (et pensez à mettre à jour). Il peut cependant que vous ayez à installer à la main un package, soit pour avoir la version la plus récente, soit parce que vous n'avez pas accès au gestionnaire de packages (sur une machine où vous n'êtes pas admin).

Il faut alors savoir qu'existent sur votre machine plusieurs arborescences texmf (les répertoires où sont rangés, entre autres, les packages) : la plupart du temps, une arborescence de base, une « locale », et une « utilisateur ». Ne touchez qu'aux deux dernières. Sur une installation TeXlive/linux typique, ces arborescences sont :

/usr/share/texmf-texlive/
/usr/local/share/texmf
$HOME/texmf

Ces chemins peuvent varier, et être modifiés. Leur valeur est déterminée par des variables d'environnement que vous pouvez afficher via texconfig conf sous TeXlive/linux. Pour en savoir plus, lisez la documentation spécifique à votre distribution (cf. fin de « trouver la doc »).

La version simple de l'installation de package est celle où il suffit de copier les fichiers (dont le .sty) depuis le CTAN vers l'endroit approprié de votre disque dur. Vous pouvez placer les fichiers au choix dans le même répertoire que votre document en cours (peu recommandé), ou dans un sous-répertoire adéquat (typiquement tex/latex/package) de votre texmf personnel ou local.

Dans ce dernier cas, il vous faudra reconstruire la base de données des packages avec la commande mktexlsr (alias texhash). Vous pouvez vérifiez que votre nouveau fichier est bien trouvé par LaTeX avec la commande kpsewhich fichier.sty qui retourne la version qui sera effectivement utilisée dans le cas où il en existerait plusieurs.

La version « difficile » est celle où il faut, en plus de ce qui est expliqué ci-dessus, compiler soi-même le package et sa documentation à partir du source .dtx. C'est assez rare, et je renvoie pour ceci à la section 4.6 de la « Not so short » (lien ctan, ou bien texdoc lshort).

Le modèle de boîtes de TeX (donc de LaTeX)

Pour TeX, produire un document revient à produire des listes de boîtes (contenant éventuellement d'autres boîtes) et à les placer sur la page. C'est au moment de la visualisation que les caractères sont placés dans les boîtes et que le document ressemble à ce qui était souhaité. (Remarquons d'ailleurs qu'un caractère n'est pas toujours « vraiment » contenu dans sa boîte.)

un exemple

Contrairement à ce que suggère l'intuition, une TeX-boîte ne possède pas deux, mais bien trois dimensions : une hauteur, une largeur, et une profondeur. La troisième dimension est liée à l'existence d'une ligne de base sans laquelle il serait difficile d'aligner les caractères. On pourrait spécifier les trois dimensions de façon équivalente sous la forme : largeur, hauteur totale, et décalage. C'est ce qui est fait pour certaines commandes comme \rule et la syntaxe LaTeX manque un peu d'homogénéité sur ce point.

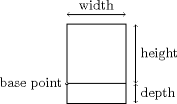
un exemple

Dans certaines circonstances (rotations de graphiques, minipage), on doit repérer un point verticalement et/ou horizontalement dans une boîte. Une convention courante est d'utiliser deux lettres, dont la première est t (haut), b (bas), c (centre) ou B (ligne de base) pour le positionnement vertical, et la deuxième est l (gauche), r (droite) ou c (centre) pour le positionnement horizontal.

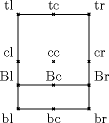
un exemple

Délimiteurs équilibrés ou non

LaTeX propose les commandes bien pratiques \left et \right pour ajuster automatiquement la taille des délimiteurs (parenthèses p. ex.) en fonction du contenu. La seule contrainte est que les délimiteurs doivent être équilibrés par paire. Voyons donc trois astuces autour de cette contrainte.

  1. On veut parfois utiliser une grande accolade ouvrante sans délimiteur fermant, pour taper un système d'équations par exemple. LaTeX propose à cet effet le délimiteur invisible « . ». Par exemple : 
    \[ (S) \left\{ % ici on ouvre... 
\begin{aligned} ax + by + cz &= 0 \\ey + fz &= 0 \\ gz &= 0 \end{aligned} 
\right. % ...et là on ferme !
\]
    un exemple
    Pour ce genre de construction, on pourra aussi utiliser l'environnement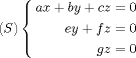 cases d'amsmath et ses variantes dcases et dcases* du package mathtools.
  2. Par ailleurs, on voudrait parfois que les délimiteurs aillent par trois (ou plus). C'est possible avec pdftex (en mode dvi aussi bien sûr, voir « ne pas confondre ») qui fournit la nouvelle primitive \middle. Cette commande s'utilise exactement comme on l'imagine : \left\{ \frac{a}{b} \ \middle|\ a \in \mathbf{Z}, b \in \mathbf{Z} \setminus \{0\} \right\} par exemple.
  3. Enfin, on ne peut parfois pas équilibrer les délimiteurs, par exemple parce que leur contenu est trop long pour être écrit sur une ligne. Il faut alors ruser en employant conjointement des délimiteurs invisibles, et si besoin des fantômes pour ajuster la taille. Par exemple : 
    \begin{align*}
a &= \left( \frac{1}{2} + b + c + \ldots \right. \\
& \qquad \left. \vphantom{\frac{1}{2}} + \ldots + x + y + z \right)^2
\end{align*}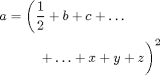
    un exemple

Ne pas confondre TeX, LaTeX, pdfTeX et pdfLaTeX

Il m'arrive parfois de parler des possibilités offertes par pdfTeX, et je crains que cela n'effraie les habitués de la chaîne dvi/ps. Une remarque rapide donc sur les rapports entre TeX, pdfTeX et LaTeX pour dissiper un éventuel malentendu.

La première chose à comprendre est que LaTeX n'est pas un programme indépendant. Ce n'est qu'un (énorme) jeu de macros pour TeX. Pour utiliser LaTeX, on pourrait en fait utiliser TeX, et commencer par lui faire lire avant notre document (avant le \documentclass) les définitions de centaines de macros. Pour des raisons d'efficacité, on utilise en fait un « format », c'est-à-dire que quand on tape latex, c'est le programme TeX qui est appelé, mais avec toutes les définitions de LaTeX préchargées.

Sur les installations modernes, ce que je viens de dire est en fait faux : ce n'est pas le programme TeX, mais pdfTeX qui est appelé. Ce dernier est une version moderne de TeX, qui possède de nombreuses fonctionnalités supplémentaires, comme la possibilité d'écrire de droite à gauche, des fonctionnalités micro-typographiques, la capacité de créer des liens hypertextes, quelques nouvelles primitives utiles (dont \middle (cf délimiteurs)) et enfin la possibilité de produire un dvi ou un pdf.

Ce dernier point justifie le nom, mais le nom prête à confusion : répétons-le, pdftex sait très bien produire des dvi. Ce qui va déterminer le mode de compilation, c'est le fait que vous l'appeliez avec latex ou pdflatex. Ces deux commandes sont respectivement équivalentes à pdftex -fmt latex test.tex et pdftex -fmt latex -output-format pdf test.tex.

En fait, la seule commande qui lancera effectivement TeX (avec le format plain) est la commande... tex ! Vous pouvez vous amuser à taper latex --version pour vous convaincre du fait que c'est bien pdftex qui travaille, même en mode dvi. Chez moi, aujourd'hui (2007-06-11), la sortie est la suivante.

$ latex --version
pdfTeX using libpoppler 3.141592-1.40.3-2.2 (Web2C 7.5.6)
kpathsea version 3.5.6
[...]

Quelques explications : 3.141592 est le numéro de version actuel de TeX, sur lequel est basé pdfTeX. Le source de TeX étant écrit en Web, un langage de programmation et documentation (notion de « literate programming ») formé d'un mélange de Pascal et de TeX, il est commode pour le compiler partout de le traduire d'abord en C : c'est le travail de Web2C. Par ailleurs, pdftex intègre désormais les fonctionnalités d'une autre extension de TeX, eTeX (version 2.2), et son numéro de version actuel est le 1.40.3 restant. Enfin, kpathsea est une bibliothèque de recherche qui aide TeX à trouver rapidement ses fichiers dans vos arborescences texmf compliquées (cf « installer ses packages »).

\def vs \newcommand

Une activité essentielle dans l'usage de (La)TeX est la définition de macros. Pour cela, LaTeX propose des méthodes qui lui sont propres (\newcommand, \renewcommand, etc.) en plus des méthodes de TeX qui restent disponibles. Comme souvent, on a intérêt sauf raison particulière à préférer les méthodes de LaTeX pour définir les commandes.

La première raison est que LaTeX opère beaucoup d'opérations de contrôle pour vous empêcher de tout casser par maladresse. En l'occurrence, le danger est de redéfinir sans le savoir une commande qui existe déjà (vous ne connaissez sans doute pas par coeur la liste des 300 primitives de TeX et encore moins celle des commandes LaTeX). S'il s'agit d'une commande ayant un rôle essentiel (comme \par ou \output), les conséquences peuvent être catastrophique et difficiles à comprendre.

Pour cela, LaTeX distingue la définition d'une nouvelle commande qui se fait avec \newcommand de la redéfinition qui se fait avec \renewcommand. Par ailleurs, il faut savoir qu'en LaTeX il est dangereux de définir des commandes dont le nom commence par \end car elles sont utilisée en interne par les environnements. Là aussi, \newcommand se charge de la vérification et vous évite des problèmes.

Par ailleurs, une raison un peu plus personnelle de préférer \newcommand est sa syntaxe plus simple pour la spécification du nombre d'arguments, et en un sens plus puissante avec la possibilité de rendre optionnel le premier argument. Concernant les arguments, \def offre d'autres possibilités, comme les arguments délimités, dont on a rarement besoin sauf pour des techniques un peu avancées.

Dans les rares cas où on a vraiment besoin de \def (ou d'autres commandes TeX comme \let ou \edef), un usage prudent est de faire précéder la définition de la macro (par exemple \def\macro) par un \newcommand\macro{} pour vérifier qu'on est bien autorisé à définir \macro.

Bien nommer ses macros et environnements

La première chose chose à savoir pour nommer ses macros où environnements est quels sont les noms autorisés. Pour les macros, ils sont de deux types : les caractères de contrôle et les mots de contrôle. Dans un caractère de contrôle (p. ex. \!), la contre-oblique est suivie d'un unique caractère qui n'est pas une lettre. Dans un mot de contrôle, la contre-oblique est suivie d'une suite de lettres et le nom de la commande se termine au premier caractère non-lettre (typiquement un espace ou une accolade).

TeX reconnaît les 52 caractères auxquels vous pensez comme des lettres. En particulier, A et a sont différents, et é, @ ou 1 ne sont pas des lettres. On peut parfois demander à TeX de changer sa notion de lettre : voir par exemple le cas de \makeatletter.

Pour les noms d'environnements, c'est plus simple : les caractères autorisés sont les lettres et le caractère * et ce, quelle que soit la longueur. Vous pouvez essayer d'utiliser d'autres caractères comme des espaces, cela marchera sans doute. Cependant, il n'est écrit nulle part dans le manuel que ça doit marcher, donc il n'est pas certain que cela marchera encore à l'avenir et je vous conseille de ne pas le faire.

Le deuxième élément à prendre en compte est le sens du nom. Même si je suis le premier à ne pas (toujours) suivre ce conseil, je vous encourage à ne pas le choisir trop court : votre source gagnera en lisibilité, et c'est sans doute plus important que d'économiser quelques frappes de touches. Par ailleurs, choisissez toujours un nom qui se rapporte au sens de la commande et pas à sa mise en forme (par exemple, \lebesgue pour la mesure de Lebesgue, indépendamment du fait que vous la notiez lambda ou autre chose).

Définir des variantes étoilées

Vous l'avez sans doute remarqué, beaucoup d'environnements ou commandes standard de LaTeX existent sous une variante étoilée. Vous pouvez avoir envie de reprendre cette idée quand vous définissez vos commandes et arguments, et j'approuve cette envie. Voyons comment la mettre en oeuvre.

Si vous avez lu l'astuce sur le nommage, vous aurez compris que c'est immédiat pour les environnements car l'étoile est un caractère autorisé dans les noms d'environnements. Il vous suffit donc de faire \newenvironment{myenv} et \newenvironment{myenv*} avec les définitions souhaitées.

Pour les commandes, c'est plus compliqué car l'étoile ne peut pas faire partie du nom de la commande. Il y aura donc une commande, qui devra être capable de regarder si elle est ou non suivie d'une étoile et d'adapter son comportement en conséquence. Pour des raisons techniques, cette commande ne pourra pas accepter d'argument, mais pourra faire appel à des commandes qui en acceptent (voir le début de « gérer ses arguments »). Par ailleurs, on utilise une commande interne du noyau LaTeX et vous pouvez vous reportez à « \makeatletter » pour comprendre pourquoi cela implique son usage.

\newcommand*\mycommandstared[1]{ciel #1 étoilé}
\newcommand*\mycommandunstared[1]{ciel #1 non étoilé}
\makeatletter
\newcommand\mycommand{\@ifstar{\mycommandstared}{\mycommandunstared}}
\makeatother

Dans cet exemple (stupide), vous pouvez alors utiliser \mycommand comme une commande avec un argument obligatoire et admettant une variante étoilée. Ainsi, \mycommand{bleu} composera « ciel bleu non étoilé » tandis que \mycommand*{nocturne} composera « ciel nocturne étoilé ».

Gérer astucieusement ses arguments

Dans cette astuce, je suppose que vous connaissez déjà la syntaxe de \newcommand. En particulier, vous savez sans doute qu'on ne peut définir (au plus) qu'un argument optionnel et que celui-ci est nécessairement le premier. L'objet de la présente astuce est de contourner, dans certains cas, cette limitation.

Commençons par une remarque assez fondamentale sur la façon dont TeX gère les macros. D'abord, il faut bien comprendre qu'une macro n'est pas une fonction : il ne s'agit pas d'exécuter à part le code de la macro et de renvoyer un résultat, mais juste de remplacer le nom de la macro par son texte de définition. En particulier, TeX n'opère aucun contrôle sur le texte de définition d'un macro, qui peut contenir des macros non définies ou n'ayant pas le bon nombre d'arguments.

On peut alors méditer sur le cas d'une commande définie comme \newcommand\latin{\textit}. Techniquement, elle semble être une macro sans argument. En pratique, l'utilisateur écrira \latin{id est} comme si la commande admettait un argument : celui-ci sera en fait passé à \textit. Vous êtes maintenant prêts à comprendre l'exemple suivant.

\newcommand*\xvec[1][0]{x_{#1},\ldots,\xvecint}
\newcommand*\xvecint[1][n]{x_{#1}}

\xvec       % donne x_0,\ldots,x_n
\xvec[1]    % donne x_1,\ldots,x_n
\xvec[1][m] % donne x_1,\ldots,x_m
\xvec[m]    % donne x_m,\ldots,x_n (attention)

Deux remarques. Si le dernier argument est optionnel et que vous ne l'utilisez pas, votre commande va manger les espaces qui la suivent, soyez prudent hors du mode mathématique. Pour des traitement plus compliqués, vous devrez utiliser des définitions emboîtées pour faire circuler les arguments entre vos différentes macros internes.

Être ou ne pas être une lettre : le cas de @

Pour apprécier cette section, vous devez avoir lu le paragraphe sur les noms de commandes. Vous savez alors qu'en temps normal, si l'on écrit, par exemple \today@midnight, il ne s'agit pas d'un nom de commande seul, mais de la commande \today suivie des caractères @, m, i, etc.

Si pourtant vous lisez les sources d'un package, d'un fichier de classe, voire du noyau LaTeX, vous constaterez que beaucoup de noms de commandes y contiennent au moins un @. Il s'agit d'un convention standard de LateX (déjà utilisée par le format plain d'ailleurs) qui sert à « protéger » certaines commandes en les rendant inaccessible à l'utilisateur en temps normal.

Ceci repose que le fait qu'on peut demander à TeX de considérer @ (ou tout autre caractère) comme une lettre si on le désire. Par défaut avec LaTeX, @ est une lettre à l'intérieur des fichiers de style (packages) ou de classe, et n'est pas une lettre dans les documents. Pour certains cas, vous pouvez vouloir utiliser des commandes internes. Il faut alors auparavant dire à TeX de considérer @ comme une lettre avec la commande explicite \makeatletter, et ne pas oublier ensuite de rétablir l'ordre naturel des choses par la commande \makeatother.

Pour un exemple d'utilisation, voir « version étoilée ».

Étoiler ses \newcommand

Une astuce qui ne changera rien à vos documents, mais rendra votre code plus robuste en vous permettant de mieux localiser les erreurs. Une des erreurs les plus courantes en tapant un document LaTeX est de mal équilibrer les accolades : en particulier d'oublier l'accolade fermante à la fin de l'argument d'une macro.

Dans un cas pareil, si rien n'est prévu, TeX lira votre fichier jusqu'à la fin avant de comprendre qu'il y a une erreur et ne pourra rien faire. Pour éviter cela, Knuth (le créateur de TeX), a prévu de distinguer deux types de macros, courtes ou longues, selon que leurs arguments peuvent ou non contenir un changement de paragraphe. Pour une raison qui m'échappe, par défaut, \newcommand définit des macros longues.

En utilisant \newcommand* pour définir votre commande, vous en faites une macro courte, ce qui est largement préférable dans la plupart des cas : ainsi, les erreurs dues à un éventuel oubli d'accolade fermante seront circonscrites à un paragraphe. En cas de problème, TeX s'en rendra compte à la fin du paragraphe (et non du document), il pourra vous signaler facilement l'emplacement de l'erreur et composer le reste du document comme si de rien n'était.

Prenez donc l'habitude d'utiliser la plupart du temps les versions étoilés de \newcommand et \renewcommand (sauf bien sûr dans des cas particuliers), cela vous épargnera quelques désagréments. (Vous pouvez vous amuser à vérifier que je suis ce conseil sur tous les exemples présentés sur cette page.)

Commenter ses fins de ligne

Une autre astuce un peu technique qui peut vous épargner bien des désagréments. Comme vous le savez peut-être, quand TeX lit votre document, il traduit chaque fin de ligne en espace. La plupart du temps (quand vous saisissez le texte d'un paragraphe sur plusieurs lignes par exemple), c'est exactement le comportement qu'il faut pour vous simplifier la vie.

Il y a d'autres circonstances où ce comportement peut être gênant. Notamment, quand vous définissez une macro un peu longue, ou que vous faites quelque chose de compliqué, vous pouvez avoir envie de présenter votre code de façon aérée sur plusieurs lignes (et indenté) pour le rendre plus lisible, comme dans l'exemple suivant.

\def\@protected@testopt#1{%
\ifx\protect\@typeset@protect
\expandafter\@testopt
\else
\@x@protect#1%
\fi}

Dans ces circonstances, vous ne voulez pas que les retours à la ligne purement liés à l'esthétique de votre code introduisent des espaces dans votre document quand votre macro sera utilisée au milieu du texte. Pour cela, prenez l'habitude d'insérer un caractère de commentaire « % » à la fin de la ligne (ce qu'on appelle souvent « commenter ses fins de ligne »).

Vous n'êtes pas obligé de commenter les fins de ligne qui suivent un mot de contrôle car, vous le savez (cf noms des macros ), les espaces sont ignorés après un mot de contrôle. Vous n'avez pas non plus besoin de commenter la fin de ligne après un chiffre qui n'est pas une spécification d'argument, car, je l'ai déjà évoqué, il est prudent de faire suivre les nombres (sauf spécification d'argument) d'un espace qui sert à les terminer, et est donc avalé par TeX comme l'espace qui termine un mot de contrôle.

Pour vous convaincre que je ne raconte pas de bêtises, que les fins de lignes introduisent bien des espaces que vous de désirez peut-être pas, et qu'on les évite facilement en commentant ses fins de lignes, je vous propose de regarder l'exemple suivant.

\fbox{
Du texte.
}
\quad
\fbox{%
Du texte.%
}
un exemple

Prenez donc l'habitude de systématiquement commenter les fins de lignes qui le nécessitent quand vous écrivez des macros ou que vous présentez du code sur plusieurs lignes. Ceci vous épargnera des désagréments qui peuvent aller bien au-delà d'un espace en trop dans votre document.